주제: 경사하강법 구현하기
오늘은 최소제곱법에 이어 경사하강법을 구현해 보고자 합니다.
*이 글에 나온 코드는 모두의 딥러닝의 예제임을 밝힙니다.
경사 하강법이란?
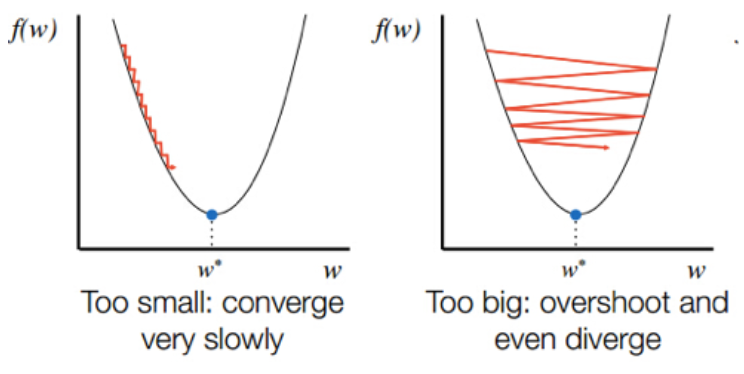
경사 하강법(傾斜下降法, Gradient descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기
(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다.
최적화할 함수 f(x)에 대하여, 먼저 시작점 x0를 정한다. 현재 xi가 주어졌을 때, 그 다음으로 이동할 점인 xi+1은 다음과 같이 계산된다.
xi+1=xi−ri∇f(xi)
이때 ri는 이동할 거리를 조절하는 매개변수이다.
이 알고리즘의 수렴 여부는 f의 성질과ri의 선택에 따라 달라진다. 또한, 이 알고리즘은 지역 최적해로 수렴한다.
따라서 구한 값이 전역적인 최적해라는 것을 보장하지 않으며 시작점 x0의 선택에 따라서 달라진다.
이에 따라 다양한 시작점에 대해 하강법을 적용하여 그 중 가장 좋은 결과를 선택할 수도 있다.
-위키백과-

CODE
import numpy as np
fake=[3, 76]
data=[[2, 81], [4, 93], [6, 91], [8, 97]]
x=[i[0] for i in data]
y=[i[1] for i in data]
def predict(x):
return fake[0]*x+fake[1]
def mse(y, y_h):
return (((y-y_h)**2).mean())
def mse_val(y, predict_result):
return mse(np.array(y), np.array(predict_result))
predict_result=[]
for i in range(len(x)):
predict_result.append(predict(x[i]))
print("공부한 시간=%.f, 실제 점수=%.f, 예측 점수=%.f" %(x[i], y[i], predict(x[i])))
print("mse 값: " + str(mse_val(predict_result, y)))
출력 값:
공부한 시간=2, 실제 점수=81, 예측 점수=82
공부한 시간=4, 실제 점수=93, 예측 점수=88
공부한 시간=6, 실제 점수=91, 예측 점수=94
공부한 시간=8, 실제 점수=97, 예측 점수=100
mse 값: 11.0
소감
경사 하강법이 생각보다 어렵지 않다는 것을 알게 되었다. 옛날에는 알고리즘이라고 하면 막연하게 어려운 것이라고만 느껴졌는데 책의 예제를 통해 하나하나 실현해 나가니 따라갈 만 했다.
'정보 과학융합탐구' 카테고리의 다른 글
| C언어로 모스부호를 익힐 수 있는 프로그램을 만들어 보자! (1) | 2024.12.04 |
|---|---|
| Famous Scientists by Balenciaga (발렌시아가 밈 패러디) (2) | 2024.08.12 |
| 최소제곱법 구현하기 (0) | 2023.07.04 |
| 9박 7일간의 차원여행 후기 (1) | 2023.06.01 |
| python을 이용하여 말머리성운의 fits파일 구현하기 (0) | 2023.05.19 |